models-and-methods:ti-dec-mdp

Transition (and Observation) Independent Decentralized MDP (TOI-Dec-MDP)

The TOI-Dec-MDP, introduced by Becker, Zilberstein, Lesser, and Goldman [1] was one of the first subclasses of Dec-POMDPs developed expressly with the intention of gaining traction on structured problems. It introduces several key assumptions that limit the mode by which agents interact. The TOI-Dec-MDP is a factored model, where the world state 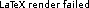$s$ comprises each agent's local state 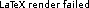$s_i$ , which the respective agent observes directly. An agent's actions cannot affect the transitions or observations that another agent experiences, but it can affect the joint reward. Hence the agents remain coupled and must coordination their actions in order to maximize their joint value.

Operationally, the TOI-Dec-MDP representation accommodates a joint reward structure defined over agents' events (local transitions or combinations thereof) [1,2].

Though seemingly restrictive, the authors argue that the TOI-Dec-MDP is expressive enough to capture a wide variety of practical interactions, including temporal constraints.

Motivating Problems

The TOI-Dec-MDP is motivated by problems involving agents that must act autonomously (from one another) with no communication, and cannot interfere with one another's actions, yet still should coordinate planned activities so as so maximize joint objectives. The two application domains that the authors reference are planetary explorations rovers selecting which sites at which to collect data and UAVs performing reconnaissance. In both domains, the objectives involve a maximization of information collected by the agents, which can only be achieved by the agents coordinating so as to avoid redundant activities.

Key Assumptions

Transition Independence: 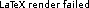$P(s_i^{t+1}|s^t,a^t)=s_i^{t+1}|s_i^t,a_i^t)$ [2]
Observation Independence: 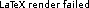$P(o_i^{t+1}|s^t,a^t,s^{t+1})=P(o_i^{t+1}|s_i^t,a_i^t,s_i^{t+1})$ [3]
Local Full Observability: $\forall o_i, \exists s_i \text{ s.t. } P(s_i|o_i) = 1$ [2]

Theoretical Properties

The TOI-Dec-MDP is NEXP-complete [2,3].

Solution Methods

Coverage Set Algorithm (CSA) [1,2]
Mixed Integer Linear Programming [4]
Separable Bi-linear Programming [5]
(Improved) Markovian Policy Seach ((I)MPS) and Markovian Policy Graph Search (MPGS) [6]

References

[1] Transition-Independent Decentralized Markov Decision Processes. R. Becker, S. Zilberstein, V. Lesser, and C.V. Goldman. Proceedings of the Second International Conference on Autonomous Agents and Multi Agent Systems (AAMAS), 41-48, Melbourne, Australia, 2003.

[2] Solving Transition-Independent Decentralized Markov Decision Processes. R. Becker, S. Zilberstein, V. Lesser, and C.V. Goldman. Journal of Artificial Intelligence Research, 22:423-455, 2004.

[3] Decentralized Control of Cooperative Systems: Categorization and Complexity Analysis. C.V. Goldman and S. Zilberstein. Journal of Artificial Intelligence Research, 22:143-174, 2004.

[4] Mixed-integer linear programming for transit|ion-independent decentralized MDPs. Jianhui Wu, Edmund H. Durfee. AAMAS 2006: 1058-1060, 2006.

[5] A Bilinear Programming Approach for Multiagent Planning. M. Petrik and S. Zilberstein. Journal of Artificial Intelligence Research, 35:235-274, 2009.

[6] Producing Efficient Error-bounded Solutions for Transition Independent Decentralized MDPs, Jilles S. Dibangoye, Christopher Amato, Arnaud Doniec, François Charpillet. In Proceedings of the Twelfth International Conference on Autonomous Agents and Multiagent Systems, 2013.

models-and-methods/ti-dec-mdp.txt · Last modified: 2014/05/06 05:07 by stefan

Table of Contents